Erdős–Turán inequality
In mathematics, the Erdős–Turán inequality bounds the distance between a probability measure on the circle and the Lebesgue measure, in terms of Fourier coefficients. It was proved by Paul Erdős and Paul Turán in 1948.[1][2]
Let μ be a probability measure on the unit circle R/Z. The Erdős–Turán inequality states that, for any natural number n,
where the supremum is over all arcs A ⊂ R/Z of the unit circle, mes stands for the Lebesgue measure,
are the Fourier coefficients of μ, and C > 0 is a numerical constant.
Application to discrepancy
Let s1, s2, s3 ... ∈ R be a sequence. The Erdős–Turán inequality applied to the measure
yields the following bound for the discrepancy:
This inequality holds for arbitrary natural numbers m,n, and gives a quantitative form of Weyl's criterion for equidistribution.
A multi-dimensional variant of (1) is known as the Erdős–Turán–Koksma inequality.
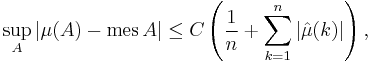
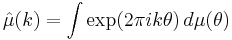
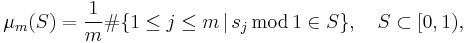
![\begin{align}
D(m) & \left( = \sup_{0 \leq a \leq b \leq 1} \Big| m^{-1} \# \{ 1 \leq j \leq m \, | \, a \leq s_j \, \mathrm{mod} \, 1 \leq b \} - (b-a) \Big| \right) \\[8pt]
& \leq C \left( \frac{1}{n} %2B \frac{1}{m} \sum_{k=1}^n \left| \sum_{j=1}^m e^{2 \pi i s_j k} \right|\right).
\end{align} \qquad (1)](/2012-wikipedia_en_all_nopic_01_2012/I/c7fcdf4ee74766f4e488dcff62f41986.png)